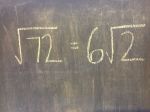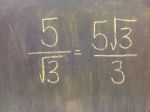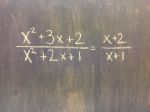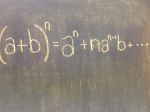The goods [#NCTMDenver]

Good turn out for my session Saturday morning (EIGHT O’CLOCK!).

Thanks to Ashli Black (@Mythagon) for the shot of title screen.

Alternate title: “Slaughtering Sacred Cows w/ Your Host, Prof. @trianglemancsd.” #NCTMDenver

— Dan Meyer (@ddmeyer) April 20, 2013

Rate of change & accumulation – BIG ideas for Middle School and beyond. @trianglemancsd #NCTMdenver

— Marc Garneau (@314Piman) April 20, 2013

We’re taking simplifying radicals, rationalizing denominators, factoring, cubics, quartics, & functions to the woodshed here. #NCTMDenver

— Dan Meyer (@ddmeyer) April 20, 2013

@trianglemancsd emphasizing experiencing ideas in informal contexts as a foundation for higher, formal math. RME everywhere! #NCTMDenver

— Raymond Johnson (@MathEdnet) April 20, 2013

Haven’t thought about rates of change, derivatives, etc in a long time. @trianglemancsd stretching my brain this morning!

— Katherine Bryant (@MathSciEditor) April 20, 2013

I’ll get some more details up here sometime soon. In the meantime, here’s the handout (.pdf). And here’s the slide deck (.zip, and which—to be honest—was just a photo album on the iPad; the simplicity of this was liberating).

Here are Alison Krasnow’s notes from the session.

One last thing…this is the absolute best form of session feedback, as far as I am concerned—getting to read someone else’s notes on the session speaks volumes about what participants experienced (in contrast sometimes to what I think we did).

The slides:

UPDATE: This talk has been adapted to a paper submitted to Mathematics Teaching in the Middle School. I’ll keep you posted on its progress.

Asking questions. Making choices.

I have had the opportunity to work this year with the wonderful staff at Laura Jeffrey Academy, a girl-focused charter school in Saint Paul, MN.

I’m still undecided on the larger questions surrounding charter schools and their relationships to public schools and public K-12 funding, so I am in no way interested in picking up that thread of discussion here.

Instead, I want to reflect on my experiences in this setting-an urban, girl-focused, open-admission middle school.

This week, I spent my first full day at the school with school in session. I had worked with the math teachers over the summer, but students are really an abstraction when we’re talking about teaching in the summertime.

As I observed a couple of classes in the morning, I was reminded of some age-old questions in mathematics teaching and learning. In particular…

Do girls like math?

This question (and its bastardized forms, Are girls allergic to algebra? Are girls too sexy for math? etc.) almost seems worth debating in the real mixed-gender world.

But spend a few hours in a Laura Jeffrey math class and it becomes obvious that these are ridiculous questions not worth wasting time with.

When you get rid of the boys, you still have just as much variation in attitudes, interests, predispositions, etc. with respect to math (and pretty much everything else) that you would in your standard mixed-gender classroom.

Of course, right?

But it is so easy to put students into categories and make blanket claims about all students in each category. Get rid of one of the two categories, though? Now we realize what a crappy way this was to categorize kids in the first place-especially if we’re trying to understand their interests, motivations and goals.

Thanks Laura Jeffrey staff and students for the reality check.

It was a pleasure and I look forward to our future work together.

Words to avoid in the middle school classroom (continued)

I have this to add to the collection so far:

Long and hard.

In trying to put the Common Core mathematical practices into kid-friendly language, a colleague transformed this:

1. Make sense of problems and persevere in solving them.

Into this:

1. Think long and hard to solve problems.

 

Words and images to avoid (addendum)

We had a little fun back in April with words and images to avoid in the middle school classroom.

Those who do not learn history are doomed to repeat it, no?

Consider the following from a recent draft of a project that will remain nameless, but which is intended for sixth grade:

Two boys who live near a golf course search for lost golf balls and package them for resale.

How many packs of 12 golf balls can be made
from a supply of 6,324 balls?

or

If a supply of 6,324 golf balls is packed in 12 boxes,
how many balls will be in each box?

QMST V: Creating an inviting classroom

Today I’m turning over the blog to a fabulous middle school math teacher who comes from an English teaching background. All those smart, smart questions from middle schoolers over the last 6 months? Her kids asked those. Give her a hand in thinking something through, would you please?

Hi.

I’m Alex Otto and I teach 7th and 8th grade math at Kodiak Middle School in Kodiak, Alaska.

I was looking for some feedback from my peers.  So much of what math teachers talk about is how to teach abstract concepts, yet so much of what is important to middle school kids is what is going on in their immediate surroundings.

Along those lines, I’m thinking about how to best arrange my classroom in terms of seating, bulletin boards, groups, “stations”, etc.  Does anyone have any ideas and especially links to pictures of “inviting” classrooms that facilitate the kind of learning that we want to take place?  (I feel like a lot of the “inviting” classrooms in my school are language arts classrooms with reading nooks, writing stations, etc. )