Pep talk for the coming school year

Here’s a transcript of something I said recently. It was in response to a common question, “That’s a great idea, but how can we fit that in when there are so many things we have to get done?”

That’s one of the things I struggle with. It’s clear to me that since I left the public school classroom in 2000, that the kinds of pressures and constraints under which teachers operate are quite a bit different. I have seen, over the years I’ve been working with teachers, a great degrading of teachers’ feelings of autonomy and ability to make meaningful decisions for their kids; particularly large decisions about curriculum, but even sometimes on a day-to-day lesson basis.

All I can say is that when I do work with teachers who are under those kinds of constraints, the thing that I try to remind them is that curriculum—whether district curriculum or published textbooks—is really a framework, and it is a teacher’s job and responsibility to flesh out that framework in ways that will create powerful mathematics learning for kids.

So I encourage you to not stray from the agreements that are necessary to make as a district or as a school—in terms of sequence of content, or basic resources we use in our classrooms—but that we have a tremendous amount of leeway in terms of setting the tone. What kinds of questions are we going to ask? What kinds of mathematical contributions are we going to value from kids?

I think it’s important for us to retain that responsibility, even when we’re feeling disempowered by forces that are outside our control.

Help some Minnesotans think something through, won’t you?

I spent some time on a conference call today as part of my duties as VP of math for MCTM. On the line were (mostly) elementary teachers and coaches. The fundamental problem at hand was beautifully stated by a participant:

If we want to grow wonderful, fabulous teachers, we have to make it easy for them to stay connected.

As the conversation proceeded, I found myself asking How does having organizations that are fixed in their physical location make sense in fostering these connections?

Several teachers described the kinds of connections and resources they would like to have access to, but that they do not (and hence why they are reaching out to MCTM and to the state department of education). These include (in no particular order):

1. Both occasional synchronous and ongoing asynchronous communication among teachers and policy and content experts;
2. Concrete resources for helping teachers move from a textbook-focused classroom to a standards-based classroom (especially a Minnesota standards-based classroom; we are not a Common Core state);
3. A place to ask about something that happened in the classroom today and to get help with what to do tomorrow as a result;
4. A way of promoting and organizing useful resources and filtering out the junk;
5. A place to have longer conversations about bigger issues such as children’s long-term development of place value concepts or current research and curricular innovations relating to subtraction; and
6. Video of classrooms in action—there seems to be a real hunger for seeing over reading classroom scenarios.

As I listened and thought about my own teaching, I became less and less convinced that a centralized resource is the answer to these needs. Indeed, the only need related to our particular state is number 2 above. But all of those other needs (and many of the general ideas underlying number 2) can be met by folks who have never set foot in our state.

I have built my own version of this support system online. Here’s how:

Blogs. Writing my own and reading those of others has generated tons of useful ideas for every aspect of my work. Just today, I took something from Chris Hunter’s blog to use with my College Algebra students, and I adapted Fawn Nguyen’s Google Form for my standards-based grading reassessment in all of my courses.

Twitter. Pretty much everyone whose blog I regularly read I also follow on Twitter. The reverse is not true, so Twitter expands my network. In the past week, I put out a general request with organizing my students’ reassessment requests and got reminded of Fawn’s system.

You know what I need? A system for organizing S reassessments. Esp. helping them focus on what they'll do to improve. Ideas? Links? #sbar

— Christopher Danielson (@Trianglemancsd) November 5, 2012

Also I have had several back-and-forth conversations with teachers on a range of topics. For example, I replied to the following…

Classic math mistake: Adding Fractions. http://t.co/hsRZfXlO

— Michael Pershan (@mpershan) November 6, 2012

Twitter facilitates a lovely combination of asynchronous resource-hunting and synchronous problem-solving. It can also be a tremendous time sink, so time management skills are essential.

Email. Back to asynchronous communication. Email for me remains a medium for having extended private conversations. I am not a fan of listservs, mailing lists or email conversations that attempt to involve more than about three people.

Experience. Having spent a couple of years in this space, I have developed a working knowledge of what’s available. I know who to ask about what’s happening at middle school, who to ask/read/recommend on assessment issues. I know who will give me a new perspective on social media use. I know who to talk to for questions about college teaching.

All of this reinforces the idea-for me-that the role MCTM could play in meeting this request from our members isn’t so much creating a space for interaction, as it could be facilitating teachers’ entry into this much larger space that already exists.

I have no idea what that would look like either, though.

How say, math-o-blog-o-Twitter-sphere?

Ratcheting back the rhetoric on Common Core

Bill McCallum writes in the comments here at OMT:

 I don’t think that effort [to define terms such “ratio” and “rate” that CCSS leaves undefined] deserves quite the ridicule it is receiving here, but never mind, the criticism will be taken into consideration nonetheless and inform the final draft. I’ll only say that if I had a dollar for every time someone told me the answers to all these questions were obvious, I’d be a rich man. Of course, the “obvious” answers are mutually self-contradictory. This seems to be an area where it is very difficult indeed to find common language, and where emotions run high.

Fair enough. I’m happy to tone things down a bit.

I do need to observe that no one here at OMT (least of all me) has suggested that the answers to the questions at hand are “obvious“. I agree that they are not obvious at all, and I agree that it is very difficult to find common language with respect to these ideas. (Although this last bit is tricky; if we all use the same words but mean different things by them, are we speaking a common language?)

No, my critique is not at all that Common Core has failed to state the obvious definitions.

My critique is that I see no evidence that Common Core-either the Standards or the Progression on rational number-take into account research on how children learn this content, nor do they seem to coincide with everyday uses of these terms. In the era of No Child Left Behind and “evidence-based practice”, I find it troublesome that results of important research work such as that in the Rational Number Project or Cognitively Guided Instruction don’t seem to form a basis for either document.

I find it surprising that there are no research references in the Progression.

In my work with Connected Mathematics, I have many times had teachers ask for definitions of rate, ratio, fraction and rational number. As writers, we have hashed out these ideas many times as well. Answers are not obvious and reasonable people can disagree.

But we sort of agree that answers to these questions ought to be consistent with, and explain relationships to, uses of these terms in mathematics and the world. I don’t understand why this isn’t the starting place for the Progression.

So how about this for a first attempt at the relationships involved here?

A ratio is a multiplicative comparison of two quantities (usually both are non-zero). Conventionally, we use the term “ratio” to apply to part-part comparisons, but this need not be the case.

We can express ratios in several forms. If there are 5 girls for every 3 boys in a certain class, we say that (1) the ratio of girls to boys is 5 to 3, (2) the ratio of girls to boys is 5:3, (3) the ratio of girls to boys is 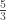, (4) there are 5 girls for every 3 boys.

The fraction notation 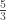 is problematic in early ratio instruction because children may confuse it to mean that  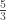of the students are girls. Children are accustomed to fraction notation being reserved for part-whole relationships; for this reason the notation should be saved for later instruction.

The term rate suggests change. We tend to talk about a “ratio” in static situations where the values remain constant but a “rate” in a situation where the quantities are changing. In the girls and boys situation above, it would be correct to say that there is a rate of 5 girls for every 3 boys, but this feels awkward. If students were enrolling in a school and there were 5 girls enrolling for every 3 boys, the term “rate” is a more natural fit.

A unit rate is a rate where one of the quantities being compared is 1 unit. If we enroll five girls for every three boys, this is not a unit rate. We could say that there are 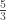 girls per boy enrolling at the school, or  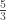girls for every boy. For every (non-zero) unit rate, there is a reciprocal unit rate. So we can also say that there are  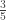boys per girl.

What counts as a unit varies. When computing a “unit rate” for buying pop, we could compute the cost per ounce, the cost per can, the cost per six-pack or the cost per case of 24. Which of these is considered a unit rate depends on our choice of unit.

To summarize the discussion, ratios and rates are different mainly in connotation. Each expresses a multiplicative relationship between two numbers (as opposed to an additive relationship, for which we use the term “difference”). Unit rates are important forms of rates because of their intimate connections to algebraic and calculus ideas such as slope and rate of change.

It’s just a first stab at discussing these terms in this context, but is consistent with common usage and focuses the discussion on the main idea that is important at this level-rates and ratios are about multiplication relationships, which are the heart of proportional reasoning.

Going back to the lawn example that has been the focus of discussion here as well as over at the Common Core Tools website, this would suggest that “7 lawns in 4 hours” is a rate (there is change involved, and it’s not a part-to-part relationship), and that there are two unit rates: 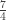lawns per hour and  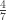hours per lawn.

Again, I am not claiming that these relationships are obvious. But if a couple of important goals for the Progressions work are (1) clarity and (2) usefulness for teachers, professional development and curriculum development, I think my proposal above is an improvement over the present document.

Your Daily Wu: Teachers and Math Educators II

wu (again) on teachers and mathematics educators (present company presumably included)

Because the flawed [mathematics] they [preservice teachers] learned as K-12 students is not exposed, much less corrected, they unwittingly inflict [this flawed mathematics] on their own students when they become teachers. So it comes to pass that [this flawed mathematics] is recycled in K—12 from generation to generation. Today, this vicious cycle is so well ingrained that many current and future mathematics educators also are victimized by [this flawed mathematics], and their vision of K—12 mathematics is impaired.

what i think he’s saying

We cannot entrust decisions about mathematics content in curriculum to anyone but mathematicians because everyone else misunderstands what mathematics is (but it’s not their fault as individuals-forgive them for they know not what they do.)

Say what? or Have you not been paying attention?

In a lengthy and rambling blog post that has made the rounds via email, Peter Wood, President of the National Association of Scholars, responds to a National Research Council Framework for K-12 science education. He concludes with a modest proposal:

What if Congress were to set aside all its efforts at curricular reform? Tell the Department of Education: Desist. Tell the states: Keep the Common Core if you like, but there will be no “Race to the Top” bonuses for adopting it. Say goodbye to “No Child Left Behind.” Tell NRC, thanks for the Framework, but we’re not in the market. Instead, Congress would pass and the President sign a bill declaring that in 2020, nine years from now, no student who scores less than “proficient” on the mathematics portion of the National Assessment of Education Progress will be eligible for a federal student grant or loan.

Oh my. Where to begin? Can we begin with an observation that drawing conclusions about individuals is not at all what the NAEP was designed for? No, it was designed (whether you believe well or poorly) to measure national progress over time. It is given to a nationally randomized sample.

Is this nitpicking? Not when the proposal comes from the President of the National Association of Scholars (whatever that is, it seems reasonable for proposals from its president to undergo a modicum of intellectual rigor).

But this isn’t what draws me to write today. No it’s his predictions for the consequences should such a proposal be enacted:

1. The rate of math “proficiency” would zoom, well before 2020.
2. Educrats would do all in their power to dumb down the test and hollow out the meaning of “proficient.”
3. Schools would declare the standard onerous and destructive; and then miraculously make it work.
4. Colleges would find a large new source of students both capable of and eager to study the sciences.
5. The incidence of “dyscalculia” would drop precipitously.

The proposal bears an uncanny resemblance to No Child Left Behind. This demanded 100% proficiency by 2014 or districts, schools and teachers would face substantial consequences. How has this worked out? Let’s break it down.

1. Has the rate of math proficiency zoomed well before 2014? No. It was 26% in 2000 and 34% in 2009. Eight percentage points in 9 years.

2. Have educrats done all in their power to dumb down the tests? No. Whether you like Common Core or not; it’s certainly tough to make the case that CCSS represents a dumbing down of standards. Cheating at the school and district level, though? That’s something different, I’m afraid.

By the way, what is an educrat? Am I an educrat? Is Peter Wood?

3. Have schools declared the standard onerous and destructive? Yes. Have they miraculously made it work? No. Have you paid any attention to No Child Left Behind at all? Seriously. Saying it doesn’t make it so. This should be the lesson of No Child Left Behind.

4. Have colleges found a new source of students eager to study science? Ummm… No.

5. Has the incidence of dyscalculia dropped precipitously? This seems to be an odd preoccupation of Dr. Wood’s. But in his own words:

As if in anticipation of the bad news, stories about “dyscalculia” seem to be getting much more play. …[V]ery few people are altogether bereft of numerical sense. How few? Four to six percent according to dyscalculiaforum.com. “At least five percent,” according to Dr. Brian Butterworth, a cognitive neuropsychologist speaking on NPR’s “Science Friday” earlier this year. “Up to 7% of the population,” says the Science Daily article I quoted. I’ve heard estimates as high as 10 percent.

So high stakes testing over the last ten years has coincided with greater attention to dyscalculia, and Dr. Wood’s prescription for the epidemic is more high stakes testing?

Dr. Wood has less confidence in his final prediction:

6.  The racial achievement gap might narrow.

It’s just that easy? Threaten African-American children with not being able to go to college unless they perform on the NAEP? That will close the achievement gap?

Oh my.