Wiggins question #7

Question 7

Most teachers assign final grades by using the mathematical mean (the “average”) to determine them. Give at least 2 reasons why the mean may not be the best measure of achievement by explaining what the mean hides.

All measures of center hide variation.

This is what makes them useful, and it is what makes them problematic.

Using the mean makes zeroes a problem in grading. Wildly divergent values (such as a zero in a gradebook) will greatly affect the mean. It is hard to argue that 2 A’s and a zero is the same as consistent D work. Yet this is how the mean plays out.

But going too far down this road will only lead to critiques of the whole system of grading students at all. I find that system to be indefensible and counterproductive. I have made my peace with it, and I try to do as little harm as possible with the responsibility I have to assign grades in my work.

All of which is to say, it is not using the mean that leads to a poor measure of achievement. It is mistaking quantitative measures for accurate ones that leads to a poor measure of achievement.

Wiggins question #6

Question 6

A catering company rents out tables for big parties. 8 people can sit around a table. A school is giving a party for parents, siblings, students and teachers. The guest list totals 243. How many tables should the school rent?

This is a classic example demonstrating the danger of applying procedures without thinking. The quotient can be expressed either as 31, remainder 3; or as . Neither of these answers the question, though. According to unspoken principles of table renting, we will probably need 32 tables.

Of course, I can imagine a student thinking like a caterer and building any of the following arguments:

• We need 31 tables (or fewer) because 5% of people on a typical guest list do not show up.
• We need 31 tables because if everyone comes, several will be young children who will sit in their parents’ laps.
• We need 31 tables—if everyone shows up, we can just stick an extra chair at each of three tables.
• We need at least 35 tables: No one wants to sit on the side where they can’t see the band playing at the front of the room, so we need to allow for fewer than 8 people at each table.
• Et cetera.

I would argue that we need to teach in ways that do two things:

1. Allow/force students to interpret their computational results in light of the context (there is a CCSS Mathematical Practice standard about this), and
2. Focus students’ attention on the role the computation plays in answering this kind of question. Why are we dividing? and What does the quotient mean? are the kinds of questions I have in mind here.

Wiggins question #5

Question 5

“Multiplication is just repeated addition.” Explain why this statement is false, giving examples.

Now this is when things get sticky.

It is a strong and presumptuous claim to say what an idea is.

In recent years, I have come to an understanding of why repeated addition is not the strongest foundation on which to build the idea of multiplication. But that is a far cry from making claims about what it is.

You see, any rich enough mathematical idea has multiple meanings. What is subtraction? Is it the inverse of addition? Is it the distance between two points on a number line? Is it takeaway? Subtraction is all of these, sort of.

And what is a fraction? The only definition of a fraction that is good enough to withstand the test of time and mathematical scrutiny is that a fraction is an equivalence class resulting from the equivalence relation,

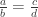if and only if

Is that what a fraction is?

No. But I am off task.

I suspect that my answer may vary from some others out there. (Although perhaps it will not.)

Repeated addition is shaky ground for establishing multiplication because it doesn’t capture the unique structure that multiplication represents.

There is additive structure, and there is multiplicative structure. Additive structure is about comparisons and changes involving the same units. Apples plus apples gives apples. Miles plus miles give miles.

Multiplicative structure is about comparisons and changes involving different units. Hours times miles per hour gives miles. Three different units; one of them a unit rate. Always.

These are related structures but they are different.

Multiplicative structure is captured better by this idea: 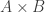means A groups of B (I am pretty sure I first ran across this particular characterization in Sybilla Beckmann’s textbook for math courses for elementary teachers). A, in this interpretation, is expressed in one unit. B is the unit rate (things per group). The product is expressed in a third unit.

This difference shows up in the following conversation between a mom and her daughter as they count the number of things in this array of meatballs.

Image from The New York Times.

Maya counted the top and bottom, 4 + 4 = 8. Then she counted L and R. 3 + 3 = 6. 8 + 6 = 14. 14 + 2 in the middle = 16. When I asked her why, she said, “Because you double count the corners when you count an array.”

She asked me to count so she could show me how. I counted 4 across the top and 3 down the side. “See, Mommy! You’re counting the corner one twice.”

 

Why do we count the corner one twice in this scenario? This seems to violate a fundamental principle of counting—one-to-one correspondence. One number word for each object, and one object for each number word.

The answer is that mom really did not count the corner meatball twice. The first time, she counted the meatball to establish that each row has 4 meatballs. The second time, she counted the rows. There are 3 rows, so there are 3 groups of 4 meatballs.

Much, much more on arrays in many places in my writing. Especially these:

Beyond the textbook wrap up (or What does this have to do with mathematics?)

Twister (on sister site, Talking Math with Your Kids)

 

Wiggins question #4

Question 4

Place these numbers in order of largest to smallest: .00156, 1/60, .0015, .001, .002

One sixtieth is the biggest of these, as the others are between one and two one-thousandths (or between one one-thousandth and one five-hundredth).

Then, in descending order, we have .002, .00156, .0015 and .001.

It is common that students will order the decimals this way:

.00156, .0015, .002, .001

I cannot predict where a person who does this will place one sixtieth.

Nonetheless, when we read these decimals as point zero zero one five six, we encourage students to ignore place value, and we encourage the misapplication of whole-number rules to the right of the decimal point.

We really do need to use place value language for decimals in classrooms. One-hundred-fifty-six one-hundred-thousandths.

Much, much more about this and related ideas in the Triangleman Decimal Institute posts from last fall. Short version: learning decimals is WAY more complicated than most people have any reason to imagine.

Wiggins questions #3

Question 3

You are told to “invert and multiply” to solve division problems with fractions. But why does it work? Prove it.

Oh dear. If anyone on the Internet has had more to say about dividing fractions than I have, I am unaware of who that is. (And, for the record, I would like to buy that person an adult beverage!)

Unlike the division by zero stuff from question 1, this question is better tackled with informal notions than with formalities. The formalities leave one feeling cold and empty, for they don’t answer the conceptual why. The formalities will invoke the associative property of multiplication, the definition of reciprocal, inverse and the multiplicative identity, et cetera.

The conceptual why—for many of us—lies in thinking about fractions as operators, and in thinking about a particular meaning of division.

1. A meaning of division

There are two meanings for division: partitive (or sharing) and quotative (or measuring). The partitive meaning is the most common one we think of when we do whole number division. I have 12 cookies to share equally among 3 people. How many cookies does each person get? We know the number of groups (3 in this example) and we need to find the size of each group.

When dividing by a fraction, partitive division means that we know the fractional part of a group we have, and we need to find the size of a whole group.

I can mow 4 lawns with of a tank of gas in my lawnmower is a partitive division problem because I know what  of a tank can do, and I want to find what a whole tank can do. So performing the division  will answer the question.

2. Fractions as operators

When I multiply by a fraction, I am making things larger (if the fraction is greater than 1), or smaller (if the fraction is less than 1, but still positive).

Scaling from (say) 5 to 4 requires multiplying 5 by . Scaling from 4 to 5 requires multiplying by . This relationship always holds—reverse the order of scaling and you need to multiply by the reciprocal.

putting it all together

Back to the lawnmower. There is some number of lawns I can mow with a full tank of gas in my lawnmower. Whatever that number is, it was scaled by to get 4 lawns. Now we need to scale back to that number (whatever it is) in order to know the number of lawns I can mow with a full tank.

So I need to scale 4 up by .

Now we have two solutions to the same problem. The first solution involved division. The second solution involved multiplication. They are both correct so they must have the same value. Therefore,

There was nothing special about the numbers chosen here, so the same argument applies to all positive values.

We have to be careful about zero. Negative numbers behave the same way as positive numbers in this case, since the associative and commutative properties of multiplication will let us isolate any values of  and treat everything else as a positive number.

More on partitive fraction division here.

Please note that you do not need to invert and multiply to solve fraction division problems. You can use common denominators, then divide just the resulting numerators. You can use common numerators, then use the reciprocal of the resulting denominators. Or you can just divide across as you do when you multiply fractions. The origins of the strong preference for invert-and-multiply are unclear.