The tale of Tabitha and the two division problems

Consider these two division problems:

Problem A: 22 cookies. Each kid gets 10 cookies. How many kids can get a full share? How many are left over?

Problem B: 22 cookies. There are 10 kids. How many cookies does each kid get? How many are left over?

These are not copied verbatim from Tabitha’s third-grade homework this week, but the numbers and context are the same. (Forgive me; I didn’t think about the potential for large-group discussion until the homework went back to school.)

The point is this: One of these problems was very easy for Tabitha, and the other was very challenging.

Do you know which is which?

We talked about this on Twitter today. (Click through for some really outstanding discussion….seriously.)

I have written about the two major types of division problems before, and they are relevant here.

Problem A was a snap for Tabitha. She skip counts well, and she is a whiz with place value. How many 10s in 268? Why 26 of course! This is the sort of thing I’m talking about.

So Problem A above is a piece of cake for her. This problem—for Tabitha—is very clearly asking How many tens are in 22? For her, this isn’t really even a question worth asking. Each kid gets one ten. There are two tens. QED.

Problem B doesn’t submit to this strategy in an obvious way. It requires her to keep track of 22 things as they get shared among 10 kids. One for you, one for you, one for you, etc. That’s taxing work, and so it’s a much harder problem for her.

When we discussed this problem together the other night, I made the argument that you use up 10 cookies each time you give everybody one cookie. I wanted to help her see how her strategy from Problem A would be useful in Problem B, while respecting that—for her—the sameness of these two problems is not at all obvious.

What’s the moral of the story? Let me know your thoughts in the comments.

The Twin Cities Shapes Tour

I recently put out a call for K—2 classrooms in which I could talk shapes with students. As a result each of the next several Mondays (Presidents’ Day excluded), I will be in a different early elementary classroom somewhere in the Minneapolis/St Paul metro area.

Last week I was at two schools: Dowling in Minneapolis and Echo Park in Burnville. I talked with one kindergarten class, three first grade classes and four second grade classes. I have learned a lot.

In particular…

Young children find composing and decomposing shapes to be much more compelling than adults tend to. They nearly all saw the bottom-right figure here as being a square and four circles. Adults can see that, of course, but we are more likely to think “not a polygon”.

On that note, I am now quite certain that we spend way too much time having young children sort polygons from non-polygons. That bottom-right shape has many more interesting properties than that of not being a polygon.

For example, a class of second graders on Friday were variously split on the number of “corners” that shape has. Is it 0, 4 or 8? Second graders can understand each other’s arguments for and against these possibilities.

These arguments can lead to the reason that mathematicians use vertex instead of corner. “What exactly is a vertex?” is a much richer and meatier mathematical question than “How many vertices does this shape have?” But if that latter question only comes up with respect to convex polygons, then it is unproblematic and not interesting for very long.

So imagine for just a moment that the lower-right figure has 8 vertices (and it wouldn’t be too difficult, I now believe, to get a classroom full of second graders to agree to this perspective, whether it agrees with the textbook definition of vertex or not).

Now kids can work on stating exactly what makes a vertex.

And what makes a vertex is going to be awfully close to what makes a point of non-differentiability (large point at apex of figure below).

I’m telling you: in twenty minutes with second graders, we can get very close to investigating things that are challenging for calculus students to describe. My point is that second graders are ready to do some real mathematics, and that sorting polygons from non-polygons is not the road to it.

Other things I found interesting:

• When kids give us something close to the answer we expect, it is easy to fool ourselves into thinking they understand. Example: on the page below, one boy said about the lower left shape that “if you tip your head, it’s a square.” A couple minutes later, it occurred to me that there might be more to the story. I asked whether the shape is a square when your head isn’t tipped, or whether it only becomes a square when you tip your head. He confirmed that it’s the latter.

• Another second grade class was unanimous that the one in the lower right doesn’t belong because it’s not a square. When I asked “is the lower left now a square, or does it only become a square when you tip it?” the class was evenly split. This was surprising to both me and the classroom teacher.

• Diamondness is entirely dependent on orientation in the mind of a K—2 student.

• The 1:1 correspondence of sides of sides to vertices in polygons is not at all obvious to young children. I sort of knew this but saw it come up again and again in our work.

• A first grader said that the spirals below didn’t belong with all the other shapes we had seen that day because “you can’t color them in”.

Even the unshaded ones that had come before could have been colored in, you see. These spirals you cannot color in even if you try. What a brilliant and intuitive way into talking about closed figures—those that can be colored in.

 

Building a better shapes book

Just a quick note here for the folks who are (a) not on Twitter and (b) not following Talking Math with Your Kids.

I created a shapes book for all ages. The digital version is free for now. Details are in this post over at TMWYK.

Standard algorithms unteach place value

I found a page full of computations sitting around the house this evening. Naturally, I picked it up and gave it a look.

Griffin (10 years old, 5th grade) had been doing some multiplication in class today. Somehow his scratch paper ended up on our couch.

Here is one thing I saw.

Naturally I wanted to ask the boy about it. He consented.

Me: I see you were multiplying 37 by 22 here.

Griffin (10 years old): Yeah. But I got it wrong so I did it again with the lattice.

Me: How did you know you got it wrong?

G: I put it in the answer box and it was wrong.

It turns out they were doing some online exercises. There is an electronic scratchpad, which he found awkward to use with a mouse (duh), plus his teacher wanted to be able to see their work, so was encouraging paper and pencil work anyway.

I was really hoping he would say that 37 times 22 has to be a lot bigger than 202. Alas he did not.

Anyway, back to the conversation.

Me: OK. Now 37 times 2 isn’t 101. But let’s imagine that’s right for now. We’ll come back to that.

G: Wait. That’s supposed to be 37 times 2? I though you just multiplied that by that, and that by that.

He indicated 7 times 2, and then 3 times the same 2 as he spoke.

Me: Yes. But when you do that, you’ll get the same thing as 37 times 2.

A brief moment of silence hung between us.

Me: What is 37 times 2?

G: Well….74.

Let us pause to reflect here.

This boy can think about numbers. He got 37 times 2 faster in his head than I would have with pencil and paper. But when he uses the standard algorithm that all goes out the window in favor of the steps.

THE STEPS WIN, PEOPLE!

The steps trump thinking. The steps trump number sense.

The steps triumph over all.

Back to the conversation.

Me: Yes. 74. Good. I like that you thought that out. Let’s go back to imagining that 101 is right for a moment. Then the next thing you did was multiply 37 by this 2, right?

I gestured to the 2 in the tens place.

G: Yes.

Me: But that’s not really a 2.

G: Oh. Yeah.

Me: That’s a 20. Two tens.

G: Yeah.

Me: So it would be 101 tens.

G: Yeah.

I know this reads like I was dragging him through the line of reasoning, but I assure you that this is ground he knows well. I leading him along a well known path that he didn’t realize he was on, not dragging him trailing behind me through new territory. We had other things to discuss. Bedtime was approaching. We needed to move on.

Me: Now. We both know that 37 times 2 isn’t 101. Let’s look at how that goes. You multiplied 7 by 2, right?

G: Yup. That’s 14.

Me: So you write the 4 and carry the 1.

G: That’s what I did.

Me: mmmm?

G: Oh. I wrote the one

Me: and carried the 4. Yeah. If you had done it the other way around, you’d have the 4 there [indicating the units place], and then 3 times 2 plus 1.

G: Seven.

Me: Yeah. So there’s your 74.

This place value error was consistent in his work on this page.

Let me be clear: this error will be easy to fix. I have no fears that my boy will be unable to multiply in his adolescence or adult life. Indeed, once he knew that he had wrong answers (because the computer told him so), he went back to his favorite algorithm—the lattice—and got correct answers.

I am not worried about this boy. He is and he will be fine.

But I want to point out…I need to point out that this is exactly the outcome you should expect when you go about teaching standard algorithms.

If you wonder why your kids (whether your offspring, your students, or both) are not thinking about the math they are doing, it is because the algorithms we (you) teach them are designed so that people do not have to think. That is why they are efficient.

If you want kids who get right answers without thinking, then go ahead and keep focusing on those steps. Griffin gets right answer with the lattice algorithm, and I have every confidence that I can train him to get right answers with the standard algorithm too.

But we should not kid ourselves that we are teaching mathematical thinking along the way. Griffin turned off part of his brain (the part that gets 37 times 2 quickly) in order to follow a set of steps that didn’t make sense to him.

And we shouldn’t kid ourselves that this is only an issue in the elementary grades when kids are learning arithmetic.

Algebra. The quadratic formula is an algorithm. Every algebra student memorizes it. How it relates to inverses, though? Totally obfuscated. See, we don’t have kids find inverses of quadratics because those inverses are not functions; they are relations. If we did have kids find inverses of quadratics, they could think about the relationship between the quadratic formula:

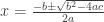
and the formula for the inverse relation of the general form of a quadratic:

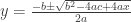
Calculus. So many formulas (algorithms) that force students not to think about the underlying relationships. If we wanted students to really think about rates of change (which are what Calculus is really about), we might have them develop a theory of secant lines and finite differences before we do limits and tangent lines. We might have Calculus students do tasks such as Sweet Tooth from Mathalicious (free throughout October!). There, students think about marginal enjoyment and total enjoyment.

On and on.

This is pervasive in mathematics teaching.

The results are mistaken for the content.

So we teach kids to get results. And we inadvertently teach them not to use what they know about the content—not to look for new things to know. Not to question or wonder or connect.

I’m telling you, though, that it doesn’t have to be this way.

Consider the case of Talking Math with Your Kids. There we have reports from around the country of parents and children talking about the ideas of mathematics, not the procedures.

Consider the case of Kristin (@MathMinds on Twitter), a fifth grade teacher, and her student “Billy”. Billy made an unusual claim about even and odd numbers. She followed up, she shared, we discussed on Twitter. Pretty soon, teachers around the country were engaged in thinking about whether Billy would call 3.0 even or odd.

But standard algorithms don’t teach any of that. They teach children to get answers. They teach children not to think.

I have read about it. I have thought about it. And tonight I saw it in my very own home.

The latest “Common Core” worksheet

You have seen this on Facebook.

My annotated version (Click to enlarge)

Ugh what a mess.

Please share the annotated version widely.

I’ll say what I have to say (comments closed) and move on. If you wish to discuss further, hit me up on Twitter or pingback to the blog. Want to talk in private? Click the About/Contact link up top.

Also, Justin Aion—middle school teacher extraordinaire—wrote up his views on the matter. You can read them over in his house.

Here goes…

The intended answer

Dear Jack,

You only subtracted 306 from 427, not 316. You need to subtract another 10 to get the correct answer of 111.

Sincerely,

Helpful student

The purpose of this task

I cannot say whether this was the right task for this child at this time because I do not know the child, the teacher or the classroom.

I can say the following:

• Analyzing errors is a useful way to encourage metacognition, which means thinking about your thinking. This is an important part of training our minds.
• The number line here is a representation of a certain kind of thinking—counting back. The number line is not the algorithm. The number line records Jack’s thinking. He counted back from 427 by hundreds. Then he counted back by ones. He skipped the tens. We can see this error because he recorded his thinking with a number line.
• Coincidentally, the calculation in question requires no regrouping (borrowing) in the standard algorithm, so the problem appears deceptively simple in its simplified version.
  
• This task is intended to help students connect the steps of the standard (simplified) algorithm with reasoning that is based on the values of the numbers involved. Why count back by three big jumps? Because you are subtracting 300-something. Why count back by six small jumps? Because you are subtracting something-something-6. Wait! What happened to the 1 in the tens place? Oops. Jack forgot it. That’s his mistake.

So what?

The Common Core State Standards do require students to use number lines more than is common practice in many present elementary curricula. When well executed, these number lines provide support for kids to express their mental math strategies.

No one is advocating that children need to draw a number line to compute multi-digit subtraction problems that they can quickly execute in other ways.

The Common Core State Standards dictate teaching the standard algorithms for all four arithmetic operations.

But the “Frustrated Parent” who signed that letter, and the many people with whom that letter resonated, seem not to understand that they themselves think the way Jack is trying to in this task.

Here is the test of that.

A task

What is 1001 minus 2?

You had better not be getting out paper and pencil for this. As an adult “with extensive study in differential equations,” you had better be able to do it as quickly as my 9-year old.

He knows with certainty that 1001 minus 2 is 999. But he does not know how to get the algorithm to make that happen.

If I have to choose one of those two—(1) Know the correct answer with certainty based on the values of the numbers involved, and (2) Get the correct answer using a particular algorithm, but needing paper and pencil to solve this and similar problems—I choose (1) every time.

But we don’t have to choose. We need to work on both.

That’s not Common Core.

That’s common sense.

[Comments closed]