As promised, more notebook pages on fraction division. This is based on the work I did a while back on trying to write authentic partitive division problems with fractional divisors. (As I wrote that last sentence, I reminded myself what a bizarre niche market I am trying to occupy on this here blog.)
I settled on situations involving fractional values of unit rates, such as the following.
If 
Before we begin, remember that if the problem were about 2 lawns in 3 hours, we would easily and naturally divide by 3. Only the numbers have changed, so the mathematical structure remains the same and we need to find 
Click each image to see it full size. If you’re into this sort of thing.
page 1
page 2
Overthinking my teaching 
What is it about fraction division that makes my brain hurt? Some models just aren’t very intuitive.
I think method #1 made the most sense to me. Some of the other methods are so abstract, I had to keep re-reading them to figure out what was going on/how it related to the context.
My mind wants to set this up as a proportion (2/3)/(3/4) = x/1, and then create common denominators by multiplying the ratio on the right by 4/3. I guess this is very similar to your method #2.
I love the extent to which you envelope the concept around context. If you were teaching this topic in a classroom, would you explore all of these different approaches?
What I really like about method 3 is that it explains why the invert and multiply rule works. When students hit middle school some of our kids have the “ours is not to reason why, just invert and multiply” mentality. Method #3
addresses it.
Fraction division with common denominators are such a great start for introducing decimal division. It seems so natural to notice how place value play a roll in creating an algorithm for decimal division. My fifth graders just explored the relationships among fraction and decimal division (using Bits and Pieces III) and it felt much more natural using common denominators. I had a few students who wanted to carried the denominator like this:
(35/10) / (7/10) = 5/10
and I am thinking that they are relating fraction division with addition and subtraction division. They all automatically understood that
(3/4) / (1/4) = 3
I would posed the question: “how many one-fourths are in three-fourths”
They said three, but one student said 3 one-fourths. I was happy that she did that. That’s precisely what I’ve been using when they try to write the answer with the same denominator as the dividend and the divisor.
We are moving onto writing algorithms for decimal division, but is there any other way to help students’ confusion when using common denominators?
You mean to refer to Method 2 I believe, Mary Dooms. If so, I agree that this is a useful thing, and missing in pretty much every textbook explanation of invert and multiply.
Iztchel, I am not sure I get your precise question here. Is it about the 3 vs. 3 one-fourths (the latter having the potential to be misinterpreted as 3/4)? If so, then I like the idea of writing answers as sentences to help keep things clear. 12÷4=3, so There are 3 groups of 4 in 12. And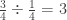
, so There are 3 one-fourths in 
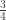. Although in this case, the fact that the divisor is a unit fraction may be more frustrating than helpful.
I was referring to method 2, but could the common denominator method be used as a “bridge” to understanding the invert and multiply rule? Or is that too abstract?
Method 1 is interesting, breaking the process into two steps like that.
Method 2 is definitely what I use for mental arithmetic but I have a harder time writing a clear explanation of what is going on, and thus a hard time explaining to kids what they should do if they don’t “get it”.
And then our good old common denominator and common numerator methods. I still find the “abstract” ratio step a lot more intuitive in the common denominator method.
Both methods are interesting.
Thank you.
I may have found another method for explaining this concept. Here is the link: http://www.greatmathsteachingideas.com/2010/12/30/dividing-fractions-the-awkward-question/ (the link near the bottom gives a series of PowerPoint slides illustrating the idea). I particularly liked this method for showing all the steps in what makes “invert and multiply” work. It shows (or at least alludes to) why we skip the other algebraic steps and end up with the rule for “invert and multiply”.
Pingback: Wiggins questions #3 | Overthinking my teaching
Pingback: Carl's Teaching Blog | Around the Blogosphere: Fractions, Grading, And A #MTBoS30 Round-Up
I like method 2, it is closest to common sense and yields the general rule.
The problem as stated can be addressed directly with common sense, as one hour is one third as much again, so multiply the original amount of lawn by one and a third (1 + 1/3) which is 4/3
This might be more trouble with nastier numbers!
Yes…this post is for a bizarre niche market, but it’s exactly what I needed! I’m reading Liping Ma’s book and realized I had no idea how to write or model partitive division with fractions, much like most of the teachers interviewed (Ch. 6). Thanks for this example, and the models you included. Much appreciated!
Yay for finding an audience! Best wishes and thanks for stopping by, chicaandbubba. Such a great book you’re reading.